Diffusion: Difference between revisions
| Line 4: | Line 4: | ||
=== The diffusion algorithm === | === The diffusion algorithm === | ||
As Russakovsky et al put it: | As Russakovsky et al put it: | ||
"In physics, the diffusion phenomenon describes the movement of particles from an area of higher concentration to a lower concentration area till an equilibrium is reached [1]. It represents a stochastic random walk of molecules" | |||
"In physics, the diffusion phenomenon describes the movement of particles from an area of higher concentration to a lower concentration area till an equilibrium is reached [1]. It represents a stochastic random walk of molecules" | |||
Inspired by the physical phenomenon of diffusion, the diffusion algorithm treats any image as an instance of the image space that has been decoded from noise. To understand this, it is worth looking at the example given by Sohl-Dickstein and colleagues (2015) who authored the seminal paper on diffusion. The author proposes the following experiment: take an image and gradually apply noise to it until it becomes totally noisy; then train an algorithm to “learn” all the steps that have been applied to the image and ask it to apply them in reverse to find back the image (see figure 1). By introducing some movement in the image, the algorithm detects some tendencies in the noise. It then gradually follows and amplifies these tendencies in order to arrive to a point where an image emerges. When the algorithm is able to recreate the original image from the noisy picture, it is said to be able to ''de-noise''. When the algorithm is trained with billions of examples, it becomes able to generate an image from any arbitrary noisy image. And the most remarkable aspect of this process is that the algorithm is able to generalise from its training data: it is able to de-noise images that it never “saw” during the phase of training. | Inspired by the physical phenomenon of diffusion, the diffusion algorithm treats any image as an instance of the image space that has been decoded from noise. To understand this, it is worth looking at the example given by Sohl-Dickstein and colleagues (2015) who authored the seminal paper on diffusion. The author proposes the following experiment: take an image and gradually apply noise to it until it becomes totally noisy; then train an algorithm to “learn” all the steps that have been applied to the image and ask it to apply them in reverse to find back the image (see figure 1). By introducing some movement in the image, the algorithm detects some tendencies in the noise. It then gradually follows and amplifies these tendencies in order to arrive to a point where an image emerges. When the algorithm is able to recreate the original image from the noisy picture, it is said to be able to ''de-noise''. When the algorithm is trained with billions of examples, it becomes able to generate an image from any arbitrary noisy image. And the most remarkable aspect of this process is that the algorithm is able to generalise from its training data: it is able to de-noise images that it never “saw” during the phase of training. | ||
Metaphorically this can be compared to a process of looking for faces in clouds (or reading signs in tea leaves). We do not see immediately a face in a cumulus, but the faint movement of the mass stimulates our curiosity until we gradually delineate the nascent contours of a shape we can begin to identify. Notice the emphasis on the virtual in the image theory underlying image generation. Noise is the precondition for the generation of any image because it virtually contains all images that can be actualised through a process of decryption or de-noising. To generate an image is not a process of creation but of actualisation (of an image that already exists virtually). | Metaphorically this can be compared to a process of looking for faces in clouds (or reading signs in tea leaves). We do not see immediately a face in a cumulus, but the faint movement of the mass stimulates our curiosity until we gradually delineate the nascent contours of a shape we can begin to identify. Notice the emphasis on the virtual in the image theory underlying image generation. Noise is the precondition for the generation of any image because it virtually contains all images that can be actualised through a process of decryption or de-noising. To generate an image is not a process of creation but of actualisation (of an image that already exists virtually). | ||
[[File:Image-diffusion-process-Sohl-Dickstein.png|alt=the process of adding noise goes from left to right and the de-noising runs the process backwards to obtain the spiral back from noise.(Sohl-Dickstein et al., 2015)|none|thumb|500x500px|The process of adding noise goes from left to right and the de-noising runs the process backwards to obtain the spiral back from noise.(Sohl-Dickstein ''et al.'', 2015)]]To learn how to generate images, algorithms such as Stable Diffusion or Imagen need to be fed with examples. These images are given to the algorithm one by one. Through its learning phase, the algorithm treats them as one moment of an uninterrupted process of variation, not as singular specimens. At this level, the process of image generation is radically anti-representational. It treats the image as a mere moment (“quelconque”<ref>For a discussion of the difference between privileged instants and “instants quelconques” see Deleuze’s theory of cinema, in particular <nowiki>https://www.webdeleuze.com/textes/295</nowiki> (find translation)</ref>), a variation among many. | [[File:Image-diffusion-process-Sohl-Dickstein.png|alt=the process of adding noise goes from left to right and the de-noising runs the process backwards to obtain the spiral back from noise.(Sohl-Dickstein et al., 2015)|none|thumb|500x500px|The process of adding noise goes from left to right and the de-noising runs the process backwards to obtain the spiral back from noise.(Sohl-Dickstein ''et al.'', 2015)]]To learn how to generate images, algorithms such as Stable Diffusion or Imagen need to be fed with examples. These images are given to the algorithm one by one. Through its learning phase, the algorithm treats them as one moment of an uninterrupted process of variation, not as singular specimens. At this level, the process of image generation is radically anti-representational. It treats the image as a mere moment (“quelconque”<ref>For a discussion of the difference between privileged instants and “instants quelconques” see Deleuze’s theory of cinema, in particular <nowiki>https://www.webdeleuze.com/textes/295</nowiki> (find translation)</ref>), a variation among many. | ||
Revision as of 17:19, 9 July 2025
Reference to Latent space.
The diffusion algorithm
As Russakovsky et al put it:
"In physics, the diffusion phenomenon describes the movement of particles from an area of higher concentration to a lower concentration area till an equilibrium is reached [1]. It represents a stochastic random walk of molecules"
Inspired by the physical phenomenon of diffusion, the diffusion algorithm treats any image as an instance of the image space that has been decoded from noise. To understand this, it is worth looking at the example given by Sohl-Dickstein and colleagues (2015) who authored the seminal paper on diffusion. The author proposes the following experiment: take an image and gradually apply noise to it until it becomes totally noisy; then train an algorithm to “learn” all the steps that have been applied to the image and ask it to apply them in reverse to find back the image (see figure 1). By introducing some movement in the image, the algorithm detects some tendencies in the noise. It then gradually follows and amplifies these tendencies in order to arrive to a point where an image emerges. When the algorithm is able to recreate the original image from the noisy picture, it is said to be able to de-noise. When the algorithm is trained with billions of examples, it becomes able to generate an image from any arbitrary noisy image. And the most remarkable aspect of this process is that the algorithm is able to generalise from its training data: it is able to de-noise images that it never “saw” during the phase of training.
Metaphorically this can be compared to a process of looking for faces in clouds (or reading signs in tea leaves). We do not see immediately a face in a cumulus, but the faint movement of the mass stimulates our curiosity until we gradually delineate the nascent contours of a shape we can begin to identify. Notice the emphasis on the virtual in the image theory underlying image generation. Noise is the precondition for the generation of any image because it virtually contains all images that can be actualised through a process of decryption or de-noising. To generate an image is not a process of creation but of actualisation (of an image that already exists virtually).
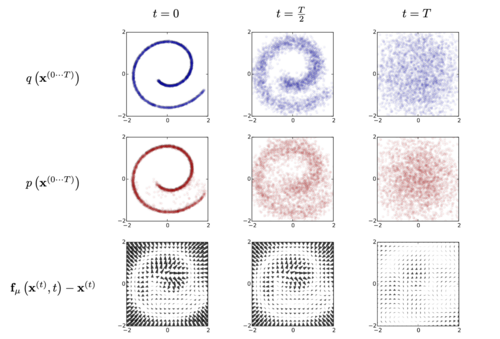
To learn how to generate images, algorithms such as Stable Diffusion or Imagen need to be fed with examples. These images are given to the algorithm one by one. Through its learning phase, the algorithm treats them as one moment of an uninterrupted process of variation, not as singular specimens. At this level, the process of image generation is radically anti-representational. It treats the image as a mere moment (“quelconque”[1]), a variation among many.
- ↑ For a discussion of the difference between privileged instants and “instants quelconques” see Deleuze’s theory of cinema, in particular https://www.webdeleuze.com/textes/295 (find translation)